 pythagoricien, em alemão pythagoreische Komma) é um intervalo de um oitavo de tom. Não é um intervalo musical autônomo. Trata-se da diferença entre duas somas: uma, de sete oitavas e outra, de 12 quintas. Embora pareça uma assunto puramente teórico, tem conseqüências práticas na construção e afinação de instrumentos de tons fixos: de teclado (piano, órgão, cravo); de trastes fixos (violão, guitarra) e de sopro com orifícios (flautas doce, transversa, clarinete, oboé, fagote).
pythagoricien, em alemão pythagoreische Komma) é um intervalo de um oitavo de tom. Não é um intervalo musical autônomo. Trata-se da diferença entre duas somas: uma, de sete oitavas e outra, de 12 quintas. Embora pareça uma assunto puramente teórico, tem conseqüências práticas na construção e afinação de instrumentos de tons fixos: de teclado (piano, órgão, cravo); de trastes fixos (violão, guitarra) e de sopro com orifícios (flautas doce, transversa, clarinete, oboé, fagote).Filolau de Crotona (470 a.C. – 399 a.C.) foi o primeiro a definir a coma pitagórica. Mas o primeiro cálculo da razão proporcional como sendo 531441:524288 encontra-se em Euclides (360 a.C. – 280 a.C.); este cálculo foi feito tendo por base a oitava com a razão proporcional 2:1 e a quinta justa com a razão proporcional 3:2.
Para ilustrar de maneira concreta gosto de fazer um paralelo com pilhas de 84 pacotes: uma organizada de 7 em 7, oura de 12 em 12. É que a quinta justa é constituída por 7 semitons e a oitava, por 12 semitons. A altura final deveria ser a mesma. Mas na afinação por intervalos justos a soma dá resultados diferentes.


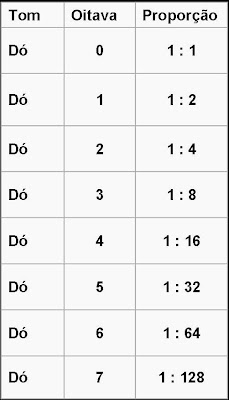
O valor da coma pitagórica pode ser extraído da tabela seguinte, na qual a superposição de 12 quintas justas, que mantém a razão proporcional de 2:3 entre suas freqüências, deveria chegar ao mesmo dó que as 7 oitavas superpostas, partindo da mesma nota inicia.

 Primeiro intervalo de quinta:
Primeiro intervalo de quinta: dó - sol
2:3.
 Segundo intervalo de quinta:
Segundo intervalo de quinta: sol - ré
4:9.
 Terceiro intervalo de quinta:
Terceiro intervalo de quinta: ré - lá
8:27.
 Quarto intervalo de quinta:
Quarto intervalo de quinta: lá - mi
16:81.
 Quinto intervalo de quinta:
Quinto intervalo de quinta: mi - si
32:243.
 Sexto intervalo de quinta:
Sexto intervalo de quinta: si - fá#
64:729.
 Sétimo intervalo de quinta:
Sétimo intervalo de quinta: fá# - dó#
128:2187.
 Oitavo intervalo de quinta:
Oitavo intervalo de quinta: dó# - sol#
256:6561.
 Nono intervalo de quinta:
Nono intervalo de quinta: sol# - ré#
512:19683.
 Décimo intervalo de quinta:
Décimo intervalo de quinta: ré# - lá#
1024:59049.
 Décimo primeiro intervalo de quinta:
Décimo primeiro intervalo de quinta: lá# - mi#
(= sib - fá)
2048:177147.
 Décimo segundo e último intervalo de quinta:
Décimo segundo e último intervalo de quinta: mi# - si#
(= fá - dó)
4096:531441.



vaaaaaalew pelo post nao entendi de primeira talvez seja quee eu nao tenha base ainda ....mas eu vou aprender
ResponderExcluir